Adding equations of two lines

In solving systems of equations by elimination method you need to add or subtract the equations of lines. Let’s take ax+by=c and dx+ey=f as equations of two distinct lines. To add equations of lines means to add the respective coefficients of x and y and the constants. It is the same as adding like terms. That is, (ax+by=c) + (dx+ey=f) = (a+d)x+(b+e)y = c+f. Of course, in solving systems of equations by elimination method you need to transform one or both equations first so you can eliminate either x or y. But that is not my concern here. I have a different problem for you involving adding equations of lines.

Problem

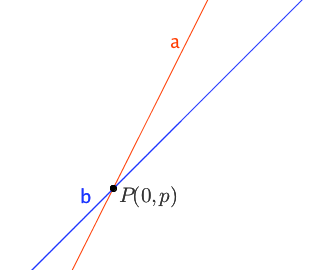
Lines a and b intersect at P(0,p). At what point will the line a+b intersect line a and line b? Can you prove your claim?

Some readers are not happy when I show the answer right away in the post. So, I’ll give you time to answer this. If you want to see my solution, e-mail me that you want access the page containing the solution or simply register to this blog.

You may also want to view solving systems of equation by elimination method for generalized version of this problem or the applet for exploring sum and difference of two equations.