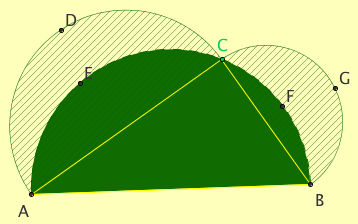
Angle inscribed in a semicircle
To solve the two problems below you need to know 1) The area of a circle is ?r2, with r as radius and that the area of a semicircle is of course half of the circle, ½?r2 and 2) the angle in a semicircle theorem.
Problem 1
Prove that the area of the solid green semicircle is equal to the total area of the two smaller semicircles ADC and CGB with diameters AC and CB, respectively.
Problem 2
Prove that sum of the area of the two crescents (the area filled with stripes) is equal to the area of the triangle ACB whose vertices are on the green semicircle.
Hint 1: Don’t google for area of crescents.
Hint 2: Answer Problem 1. Do this and you will have the shortest proof ever for Problem 2.
Enjoy these problems with your friends. Email me your answers or better, write them in the comment section.
Click the links for more problems
About The Author
