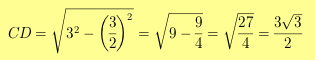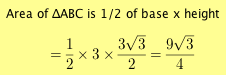Area of an Equilateral Triangle

Somebody left this in my message box:

Problem

If a triangle is an equilateral triangle with 3m and you are not given the perpendicular length of a triangle, how do you calculate the area of a triangle?

Obviously the sender know that the perpendicular length aka height or altitude of the triangle is needed to solve it. Usually textbook authors or the teachers will not specify the kind of triangle if it is not key to the problem:-). So let’s find out all the things you can know about this triangle.

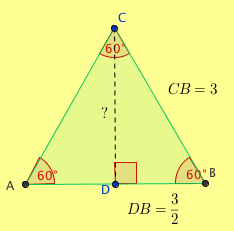
That looks perfect. DB is 3/2 because it is half of AB. The altitude to the base of an isosceles triangle (and so do equilateral triangles) bisects the base. DB is also the side opposite the 30-degree angle of the right triangle so it is half the length of the hypotenuse. The problem now is the length of CD. What is it do they say about the side opposite the 60-degree angle in a right triangle?

Can’t remember? No worries. Good ol’ Pythagoras can help us here. In a right triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides.

So,

And the area of equilateral triangle ABC is:

Now, that’s for equilateral triangle with side 3 units. Calculate the area for equilateral triangle with side a units.

These two theorems really comes in handy for dealing with right triangles so I suggest you keep these in mind. If you forget one of these, there’s always the Pythagorean theorem.

1. In a right triangle, the length of the side opposite the 30-degree angle is half the hypotenuse.
2. In a right triangle, the length of the side opposite the 60-degree angle is ?3 times the shortest side.

There are other ways of solving this problem using trigonometry and Heron’s formula.