Comparing Probabilities of Spinners
The probability of a spinner stopping at a certain area is the ratio of that area to the area of the entire region. Here is a question about comparing probabilities to test your understanding of this concept.
Problem
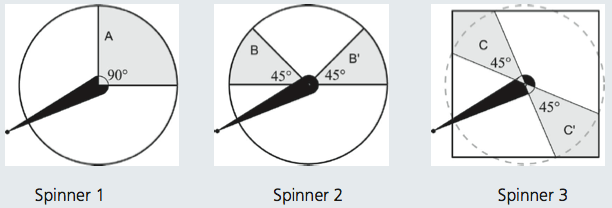
Four students are examining three spinners. They are discussing the probabilities of the spinners stopping at the shaded region.
For each of the following statements, state whether it is Completely True, Partly True or Completely False. If one sentence is true, but the other is false, check Partly True.
1. Sherry says, “The probability is twice as large for Spinners 2 and 3 compared to Spinner 1 because they have two regions to stop on and Spinner 1 has only one region.” (Completely True, Partly True or Completely False?)
2. George says, “Spinners 1 and 2 have the same probability since the shaded regions have the same area. Spinner 3, however, has a higher probability than Spinner 2 because the shaded region is a larger area.” (Completely True, Partly True or Completely False?)
3. Paul says, “Spinners 1, 2 and 3 have the same probability because the angles of the shaded regions are the same size.” (Completely True, Partly True or Completely False?)
4. Rainey says, “The probabilities for Spinners 1 and 2 are the same because those areas are the same proportion of the whole circle. For Spinners 2 and 3, however, the probabilities are different because the shaded areas for Spinner 3 are a bigger proportion of the whole square than they are of the circle.” (Completely True, Partly True or Completely False?)
Source of the question: Teacher Education and Development Study in Mathematics (TEDS-M) Policy, Practice, and Readiness to Teach Primary and Secondary Mathematics Conceptual Framework.