Describing solutions of equations

You get a full mark not only because you have the correct answer but also because you have expressed your answer in a clear and concise way using the language of mathematics. Let me illustrate it in the problems below which involve solving equations.

Problem 1

Find all the possible solution to the equation y-1 = 2x.

Answer (1/3 points)

There are many solutions to this because you can take any value for one of the unknowns/variables and then substitute it to get the value of the other.

Answer (2/3 points)

There are many solutions. For example, x=0 and y = 1, x= ½ and y = 2, x = -1 and y = -1, etc. In ordered pair form, the sample solutions are (0,1), (1/2,2), (-1,-1) etc.

Answer (full mark)

The solution is the set of ordered pairs (x, 2x+1) for any x value.

Answer (full mark)

The solution is x = t, y = 2t + 1, or the ordered pair (t, 2t + 1)where t is any number.

The last answer is very important, something that you should really try to learn. This is because sometimes we are not after all the solutions but only those that make sense to the problem. For example x may refer to the number of birds and y to the cost you need to pay. You can’t have a fraction of a bird.  So this means the correct solution would be is x = t, y = 2t + 1, where t is a whole number or nonnegative integer.

Here’s another interesting problem:

Problem 2

What are the integral solutions of the equation 5x + 2y = 8. (Integral solutions of an equation refers to solutions that are integers only. This means you find the pairs of values of x and y that are integers.)

Answer (half mark)

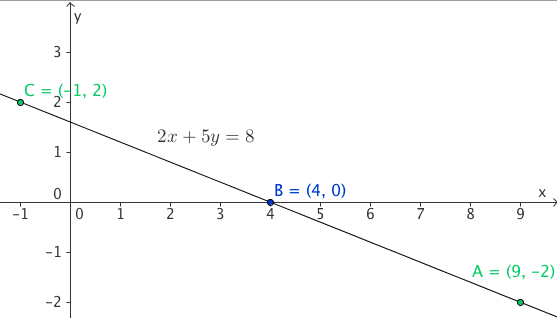
The coordinates of A, B and C are some of the integral solutions of 2x + 5y = 8

Answer (full mark)

2x+5y = 8

=>5y = 8- 2x

=>5y = 2(4-x)

This implies that 2 is a factor of y (it certainly is not a factor of 5). Therefore, y is even.

So, y = 2t where t is an integer and x = 4-5t for all integers t. (5(2t)=8-2x => x=4-5t)

You may also write the solution as (x,y)=(4-5t,2t) for all integers t.

Definition: When an equation requires only integer solutions, we call it a diophantine equation.