August 26, 2013

How to find the equation of graphs of functions

In your study of function, the usual activity you do is to graph the function given an equation. Here is a problem that involve finding the equation given the graphs of functions – linear, quadratic, exponential, and reciprocal (rational) functions.

Problem

The figure below shows the graphs of common functions. The algebraic representation of the functions are also also given. What is the equation of each graph?

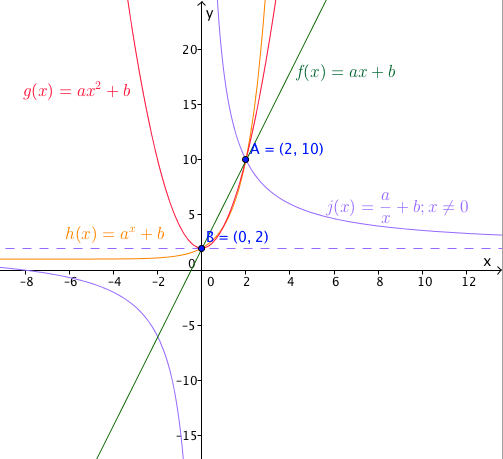
Determining the Equations of the Graphs of Functions

Did you notice that all the graphs pass through two points? Well, technically the violet one doesn’t but it’s asymptote does pass through one of the points.

Did you notice that all the equations have two parameters a and b? This means that all you need to do to find the equations of the line is to solve for the values of a and b. You can do this by substituting the coordinates of the two points A and B to the equation.

To find the equations of the line:

The line passes through (0, 2) hence the y-intercept is 2. In the equation f(x) = ax + b, b is the y-intercept hence the equation is now f(x) = ax + 2. To find x we use point A. We substitute 10 for f(x) and 2 for x. This means we now have 10 = 2a + 2. Solving for a, we have 8 = 2a or a = 4. Therefore, the equation of the linear function is f(x) = 4x + 2.

To find the equation of the parabola:

The y-intercept is also 2 which corresponds to the value of b in the equation $ax^2+b$ . To find the value of a we use the other point A. Substituting, we have $10=a(2)^2+2$ . This is equal to 10 = 4a + 2 or 8 = 4a. This gives a = 2. Therefore the equation of the parabola or the quadratic function represented by the parabola is $g(x)=2x^2+2$ .

To find the equation of the exponential function curve:

The y-intercept is 2. To find a, we substitute the coordinates (2,10) in the equation $h(x) = a^x+b$ . This gives us $10=a^2+2$ . This results to + $\sqrt8=2\sqrt2=a$ . So the equation is $h(x) =(2 \sqrt2)^x+2$ . We do not take the negative square root since the exponential function is not defined for negative base.

To find the equation of the hyperbola:

The value of b in the equation of a hyperbola corresponds to its asymptote. In the given graph the asymptote passes through (0, 2). To solve for a we also use the other point at (2, 10). This gives us 10=a/2 + 2 which simplifies to 8 = a/2. So a=16. Therefore the equation of the hyperbola is $j(x) = \frac{16}{x} + 2$ .

THINK: Are the equations unique? Are there other functions (linear, quadratic, etc) that will contain points A and B?

You may also want to learn how to match function graphs and tables.

Tags:exponential functions, linear function, quadratic function, rational functions

About The Author

lines

One Comment