Geometric Interpretation of Trapezoid Area Formula

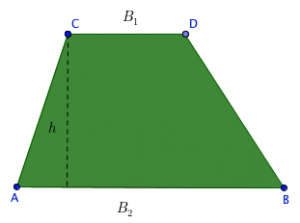
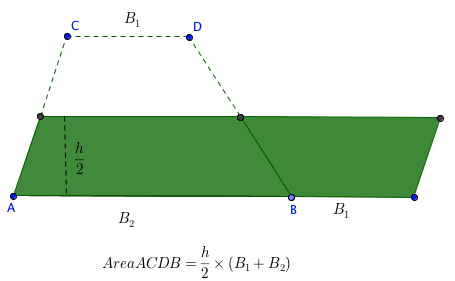
Problem 1

Show that the area of a trapezoid (trapezium) is half its height times the sum of the parallel sides.

Solution

Cut the trapezoid along the midpoints of the pair of non-parallel side. This halves its height. Rotate one of the parts 180 degrees about a midpoint. In the figure below, it’s about the midpoint of DB. The resulting figure is a parallelogram. To get the area of the parallelogram, simply multiply its base and height.

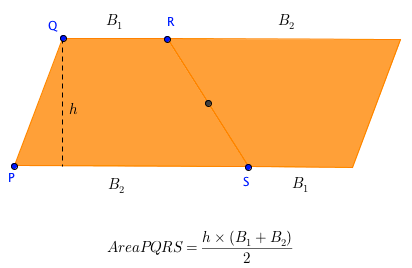
Problem 2

Show that the area of a trapezoid (trapezium) PQRS is half the sum of its parallel side times its height.

Solution

The trick is to rotate PQRS 180 degrees about the midpoint of RS. This results to a parallelogram double the size of trapezoid PQRS. To get the area of the trapezoid, halve the area of the parallelogram.

Of course the two expressions for the area of a trapezoid are equivalent. A little algebra trick will produce identical expressions. What was shown here is that each expression has its own geometrical meaning or interpretation.

Problem 3

I have constructed two more lines parallel to side PQ as shown in the figure. What algebraic expressions for area of trapezoids can be constructed from the diagram below?

If you like this post kindly share it or link back if you will use its ideas in your site. Thanks.

I made a GeoGebra applet for Problems 1 and 2 and posted it in AgIMat.