How to sketch the graph of the derivative of a function
What is a derivative function?
The derivative function f is a function f’ that maps each value of x to the gradient or slope of the line tangent to f(x). Let’s have an example. Suppose your function f is defined by f(x)=x2. The derivative of f is the function f’ defined by f’(x) =2x. This means that at point (1,3) in the graph of f(x)=x2, the gradient of the tangent at this point using the formula f’(x) = 2x is f’(1)=2(1) = 2. The gradient of the tangent line at (-1,3) is f’(-1) = 2(-1) = -2. To see how this looks like graphically and to review on the meaning of derivative click Derivative of a function. But if you want the challenge now, solve the differentiation problem below.
Problem
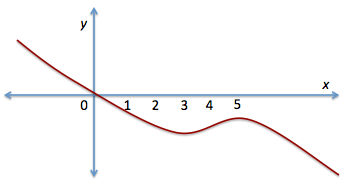
The graph of f is shown here. Which one of the following could be the graph of the derivative of it?
Discussion and Answer
Start by considering the sections of the graph that have negative gradient, positive gradient, and zero gradient. The gradient of the tangent line is negative for the part of the graph that is falling as x increases, positive for the part where it is rising and zero at the point where the change in direction occurs. This is shown in the figure below.
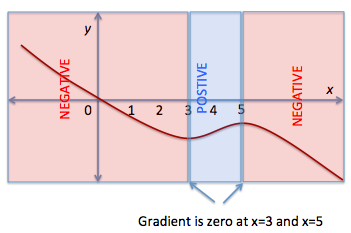
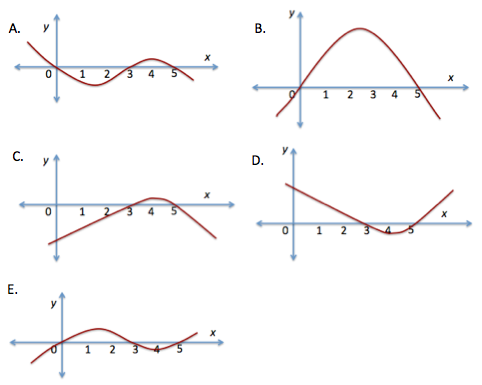
The zero gradient places will be a good start for analyzing the function. The graph of the derivative must have x intercepts at x = 3 and x= 5. This eliminates Option B. The gradient from x = 3 to x = 5 is positive and therefore the graph of the derivative must be found in the positive axis. This eliminates Options D and E. Thus the answer is C. What if the test is not multiple choice and you are asked to draw the derivative? How would you continue from here?
The gradient from left to x = 3 is negative hence the graph of the derivative must be below the x-axis. It is also negative from x = 5 to positive infinity. So your graph must look like the one in C.
Want to try another derivative problem, click slopes of tangent lines to a curve.
La question pour Léa:
– La totale: Tout comprendre, en anglais comme en math.
– La petite débloquante, pour commencer: Deviner le sens du mot “GRADIENT”.
Thank you Erlina, great making!
We share this array of concepts: basic-from-scratch, step-by-step, “realist” in the sense authors like E. Zola or H. de Maupassant inovated: Do not express what you think the actor look or feel! Just express the fact(s) and LET THE READER DEVELOP HIS(HER) OWN FEELING, REFLEXION, ETC. (i.e. participation, involvement).
You give me the incentive to contribute in this trend, in here or elsewhere.
I have several cases in head or in rough, among which one on VECTORS: The run (direction and norm of the vector) of a sailing-board, to sketch, given a direction and norm of the wind and a direction of the wichboam (segment).
I give the elements on a scan, thus you proceed the article?