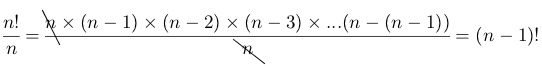Linear vs Circular Permutations

Linear permutation refers to the number of ordered arrangement of objects in a line while circular permutations is an ordered arrangement of objects in a circular manner. If you want to know for example the number of different arrangements of 5 people can sit around a circle or the number of different ways you can arrange 5 different coloured stones around a necklace, you will need to compute for circular permutation. Below are two problems that will help you distinguish arrangements of objects around a circle and arrangement of objects on a line.

Problem 1

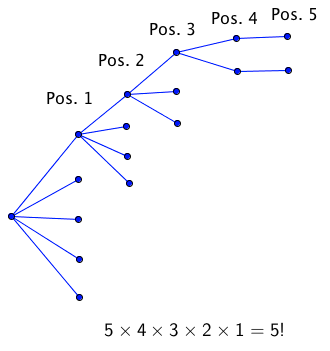
Arrange five different coloured beads in a line. How many different arrangements are there in all?

Solution

There are five possible positions of the beads on the line. There are 5 beads I can choose from. For any of the bead I put in the first position, I now only have 4 beads to choose from for the second position. For each of the previous arrangement I now only have 3 beads to choose from for the third position and so forth until the last position. The tree diagram below illustrates this. By the multiplication principle, the number of possible arrangements is 5 x 4 x 3 x 2 x 1 or 5! or 120 ways.

For n different or distinguishable objects, the number of ways of arranging them linearly is n x (n-1) x (n-2) x …1 or n!

Problem 2

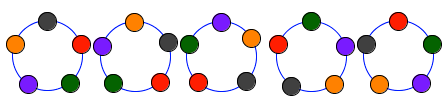
Arrange five different coloured beads around a necklace. How many different arrangements are there in all?

Solution 1

The following 5 arrangement of beads around a necklace is counted as 1 arrangement. This arrangement is black-red-green-purple-orange. You can put the black bead in the first position, second, third, fourth, and fifth and as long as it is followed by the other four beads in the same order, it will just be the same arrangement.

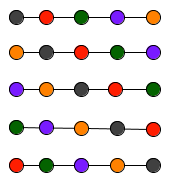
In a linear arrangement, each of this arrangement is different as shown in the image below (imagine cutting the necklace).

So, if the number of ways of arranging the 5 beads on a line is 5! or 120 ways and every 5 of these corresponds to 1 arrangement in a circular manner then the number of circular permutations of 5 different coloured beads is 5!/5 or 24 ways.

For n different or distinguishable objects, the number of ways they can be arranged around a circle is n!/n.

Solution 2

Another way to think about this is to make the problem similar to linear permutation. This can be done by choosing a fix position for one of the bead and then arrange the remaining beads in different order. Suppose the black bead is in the first position. You have 4 choices for the second position, 3 in the third, 2 in the fourth, and 1 in the fifth position. That is, having chose 1 bead for the first position, there are 4! ways of arranging the numbers in the remaining four positions in the necklace. SO the number of ways of arranging the beads around a necklace is 1×4! or simply 4! which is equal to 24.

For n different or distinguishable objects, the number of ways they can be arranged around a circle is (n-1)!.

Note that n!/n = (n-1)!

Of course problems on circular permutations get more exciting when there are restrictions in their arrangements. Watch out for this in the next few posts on this topic. For more problems view counting seating arrangement.

You may also want to learn the basics of counting and probability from former USA Mathematical Olympiad winner David Patrick.