PEMDAS Order of operation
The following photo is going viral in Facebook with 848, 039 likes as of this writing. I checked out the latest 200 comments/answers and I got the following: 20, 320, 306, 128, 116, 34, 128, 160, including “depends on the value of x“. But there should only be one answer otherwise, what’s the use of learning arithmetic if number expressions are subject to different interpretations. That’s why, mathematicians has to formulate the rules of the order of operation in around 1500s – the MDAS. This rule simply means you first do multiplication (M) and division (D) which ever one of them comes first from left to right, then do addition (A) and subtraction (S) which ever comes first from left to write. If the expression comes with exponents and parenthesis, you do the one with parenthesis first then exponentiation, P then E, followed by M or D, followed by A or S. Remember PEMDAS. But don’t forget that in the order of operation, multiplication and division have the same rank and so do addition and subtraction.
Of the last 200 answers in Facebook, the most popular is 20. Thank goodness. Most people still remember their arithmetic. So it’s not actually true that 73% failed to answer the question. But we don’t know how many of those correct answers are second tries:-)
Why 20?
4×4+4×4+4-4×4
= 16+16+4-16
= 32+4-16
=36-16=20.
Close second to the correct answer is 320. Can you figure out where they got 320?
How many squares do you see? is another Facebook math problem which is also going viral. I’m sure you will like it. Just click the link.
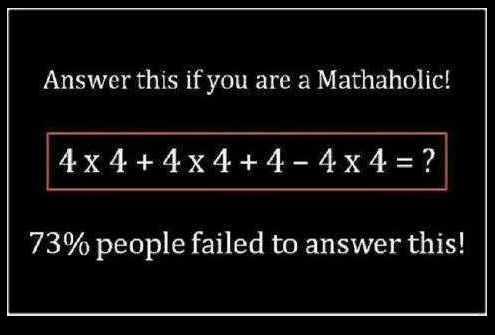
Uh duh I got this right with just my mind just follow the stupid problem! I’m in 4th grade
4-4-4-4 you have used to *,+,-,/ but answer give me 20
I’m one of 27%)))
PEMDAS may have been practical in the 1500’s, but in a modern computer/digital driven world it should no longer have any place. I agree with the sentiment that it should be isolated with brackets, making the equation unambiguous to humans, machine and/or aliens.
I don’t see how PEMDAS would work in any real life (or even computer programing, unless you actually CODED it that way) situation.
It was ‘coded’ that way 🙂
Why don’t you use brackets to isolate the multiplications making the problem unambiguous, like math used to be in the good old days?
Part of the challenge 🙂
Each to his own, I suppose. I tend to think that, if there is something simple that can be done to promote understanding, why not do it?
Not part of ANY challenge. It’s a rule. The order of operations is simple… PEMDAS
I thought mathematics was a universal language. Don’t we broadcast to the stars using it, in case anyone is listening.
It’ll be a great pity if the alien who gets the message doesn’t happen to know this arbitrary rule.
Getting 320 is due to working from left to right taking each operation as written without any understanding of order of operations. This is a regular problem with Maths students who will follow properly when specifically instructed on order but when questions come up in isolated situations revert to the 320 answer. Also a problem with algebraic questions at times such as x+5-4[x+3].