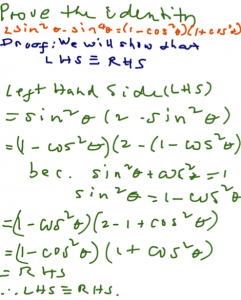Proving trigonometric identities #2

Problem:

Prove that the equation below is an identity:

2 sin²? – sin⁴? = (1 – cos²?)(1 + cos²?).

Solution

To prove that an equation is an identity, one must show that the Left Hand Side (LHS) of the equation is identical to its Right Hand Side (RHS). That is, LHS ? RHS.

Proof

LHS: 2 sin²? – sin⁴? = sin²? (2 – sin²?)

  = (1 – cos²?)(2-(1 – cos²?)). This is because sin²?=(1 – cos²?) from the Pythagorean identity sin²?+cos²?=1.

  = (1 – cos²?)(2-1+ cos²?). Remember the rule about removing signs preceded by a minus sign.

  = (1 – cos²?)(1 + cos²?)

  = RHS

LHS ? RHS. QED.

Note: This post is actually for my nephew. I hope the teacher will let him explain this. It should lessen my guilt as math teacher … and I should buy myself a stylus.

Click Proving trigonometric identities #1 for another example.