Ratio and probability problem

It is always assumed that a sample has all the characteristics of the population from which it is taken. For example, if it is given that the ratio of men to women in a population is 2:3 or 40% to 60%, the same will be true to the sample.

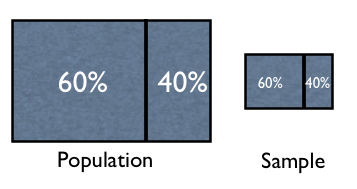Problem

A survey has shown that 40% of the citizens of Parque is against the construction of a new by-pass. If 40 of the residents are chosen at random, what is the expected number of this group who will support the construction of the by-pass?

Discussion

If your answer is 16 you were tricked. The 40% represents those  against the construction. This implies that the 60% supports it.

The 40 residents chosen at random from the population comprises the sample. This means that the same ratio of those for and against the construction of the bypass is also true to this sample. Thus, among these 40 residents, the 60% supports the construction, the 40% do not. The problem asked for the number of residents from the 40 residents chosen as sample so the answer should be 0.60 x 40 = 24.

Solution using ratio and proportion

This problem is usually classified as a probability problem. But as shown in the previous discussion you can think about it as a classic ratio and proportion problem. You can set the proportion as:

100% : 40 = 60% : x or 100% : 60% = 40 : x.

After expressing the percents to decimal this simplifies to x = 0.6 x 40 => x = 24.

Solution using probability

If you want to use the language of probability, here’s one way of solving it.

P(against construction) = 0.4

P(for construction) = 1-P(against) = 1-0.4 = 0.6 (Note that 1 represents the 100% of the population)

The number of expected residents supporting construction from a sample of 40 is 0.60×40 = 24.

Note that basic probability problems can usually be solved by proportional reasoning.