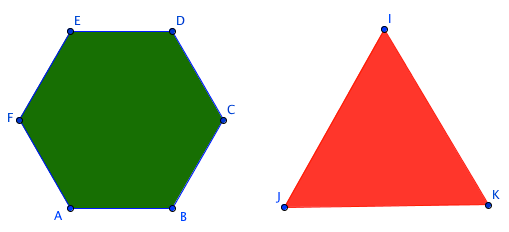
Ratio of Areas of Regular Polygons

Problem

The two regular polygons ABCDEF and JKI have the same perimeter. What is the ratio of their areas?

Solution

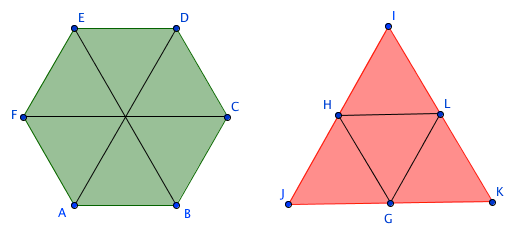
Since you are comparing areas of polygons, the most efficient solution would be to dissect them into congruent shapes. That is, show that both polygons can be tessellated or tiled by the same shape. Of course, you have to keep the condition that they have the same perimeter. This is easy to show with regular hexagons and triangles since 3, the number of sides of a triangle, is a multiple of 6,which is the number of sides of a hexagon.

Let x be the length of one of the sides of the hexagon. This implies that both polygons below have the same perimeter of 6x. So, the ratio of the area of the hexagon to the triangle (count the unit equilateral triangles) is 6:4 or 3:2.

Extension Problem 1

Suppose the ratio of the perimeter of a regular hexagon to an equilateral triangle is 1:2, what is the ratio of the area of the hexagon to the area of the triangle?

Extension Problem 2

What if the ratio of the perimeter of the regular hexagon to the equilateral triangle is 1:3? What can you say about the ratio of their areas?

Happy investigating!!!

Want another area problem? Try Area of Shaded Region.