Which rectangle has a bigger area?

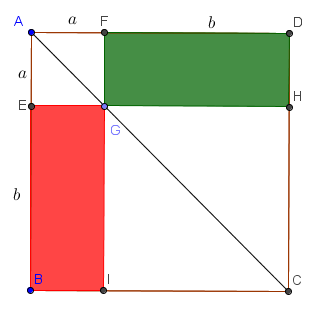
ABCD is a square and G is a point on its diagonal. Obviously, the two colored rectangles have equal area: ab.

What about in the figure below?

Problem:

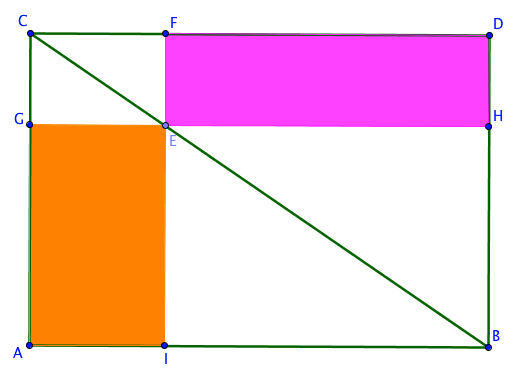
ACDB is a rectangle. E is a point on the diagonal.  Which rectangle has a bigger area? GEIA or FEHD?

Answer

The diagonal divides a rectangle into two triangles that have equal areas. This means ACB = CDB. This same diagonal CB also passes through the diagonals of rectangles CGEF and EIBH dividing them into triangles of equal area. That is  CGE = CFE and EIB = EHB. So, what you can say about rectangles GAIE and FEHD? Why?

Please share your own solution or explanation. How about the perimeter of the rectangles? Are they the same? When are they equal.