Solving problems by equations and graphs

Problems need not always be solved by equations alone. Problems that involve setting up equations can be solved using graphs also. This requires knowledge of interpreting equations in x as a function of x. This is an important knowledge as it will be handy in solving problems in calculus.  The key to the solution of course is still the correct interpretation of the problem and correct representation. Here is an example of a typical problem involving quadratic equations.

Problem

A number when squared and multiplied by six gives the same result as when twelve is added to it. What is the number?

Solution sure to get 1/5 mark

Let x be the number

6x² = 12 

x² = 2

x = +?2

To check: (+?2)² x 6 = 12

The equation 6x² = 12 is not the correct representation of the problem. The problem says “gives the same result as when twelve is added to it”. Well, you did not add the “it” to 12. That “it” is the number, your x. Anyway, you will get half mark for at least letting me know you can solve the equation 6x² = 12. You get another half for the smiley which tells me you enjoyed solving the problem.

Solutions sure to get 5/5 mark

1. Using factoring (Of course you must have the correct equation to factor first!)

Let x be the number

6x² = x + 12

6x² – x – 12 = 0

(3x + 4)(2x – 3) = 0

If 3x + 4 = 0 then x = – 4/3.

If 2x – 3 = 0, then x = 3/2.

You get 3 marks for setting the correct equation. The other four steps is worth half-point each, a total of 5.

2. By graphing

Let x be the number. The equation 6x² = x + 12 represents the problem. The equation can be transformed to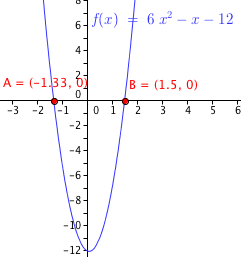 6x² – x – 12 = 0. The left hand side is a function in x that is, f(x) = 6x² – x – 12. The point at which the graph of f(x) will intersect the x – axis is the point when f(x)=0. Thus, x = -1.333 and x = 1.5.

If I’m your teacher you will get the full mark for this solution unless I explicitly said in the problem you need to solve it algebraically.

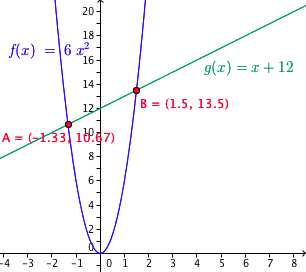
3. By graphing – systems of equation

Let x be the number. The problem says that 6x² = x + 12. This equation can be interpreted as two functions that are equal. That is, f(x) = g(x) where f(x) = 6x² and g(x) = x + 12. The points at which the graphs of these functions will intersect are the values where the functions are equal. These points are at x = -1.3333 and x = 1.5. This is shown in the graph below.

You will get the full 5 marks for this!

Remember: The more you know about how a piece of knowledge is connected to another, the more powerful and useful that knowledge is in problem solving and in understanding mathematics. Solving problems in different ways is a very good math habit.

Improve your math problem skills: