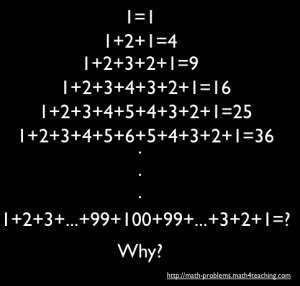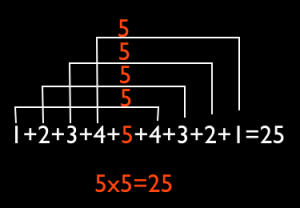Sum of Consecutive Numbers
Problem 1
Can you work out the answer to this number pattern and explain why you think you have the correct answer?
You probably observed that the sum is the square of the middle number. Can you work out why? Why do you have a square number for the sum?
Solution 1
Solution 2
Solution 3
Consecutive numbers can be represented by a stair.
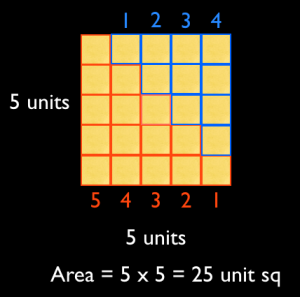
This problem of course is generalizable. Adding 1+2+ 3+ …(n-1)+n+(n-1)+…+2+1 using the three solutions gives [1+(n-1)] + [2+(n-2] + … n+0 = n+n+…(n times) = nxn = n^2.
Problem 2
You are probably familiar with Karl Friedrich Gauss. He was bored in his math class that his teacher ask him to get the sum of the first 100 numbers (1+2+3+…99+100). He gave the answer in less than a couple of minutes. Can you use the solutions above to find the sum of the first 100 counting numbers? Generalise it to n counting numbers.