Tangents to Circles Problems
Problem 1
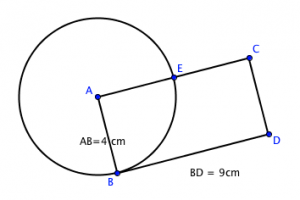
The figure below shows circle A and rectangle ABCD. The measures of segments are indicated. How long is EB?
This problem is not that hard. All you need to see is that AB and AE are radius of Circle A. Also, because ABCD is a rectangle, BD = AC. Now, all you need is Grade 1 mathematics to find the length of EC.
Here’s a more interesting problem
Problem 2:
In the figure below, DB, DE, and FG are tangents to the circle. Which is longer? The perimeter of ?DFG or the sum of line segments DB and DE?
The following visuals should help you in the solution:
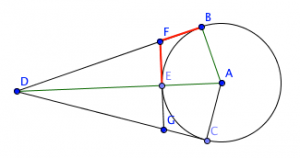 It’s easy to say the perimeter of ?DFG is the same as the sum of the lengths of DB and DE based on the figure but you will not get a full mark for that. Your teacher will ask for a proof. So how would you think about it?
It’s easy to say the perimeter of ?DFG is the same as the sum of the lengths of DB and DE based on the figure but you will not get a full mark for that. Your teacher will ask for a proof. So how would you think about it?
To prove, you have to show that FB and EA are congruent. You can do this by proving that they are corresponding parts of congruent figures. Now, where will you get those? EBAE looks like a kite. A kite is a quadrilateral where two pairs of equal adjacent sides. Before you can say that EBAE is a kite, you have to prove first that it is a kite. That is a little tough. So what else can you do? You can show that FB and FE are parts of congruent triangle. This is a little easier.
Here’s how you do it:
1. Draw FA.
2. Angle B = 90; angle E = 90. This is because they are the points of tangency. Tangents to circles make 90 degree angles with the radius at the point of intersection.
3. ?FBA and ?FEA are right triangle because they have a right angle. They share the hypotenuse FA.
4. BA = EA because they are radii of the same circle.
5. ?FBA and ?FEA are congruent by hypotenuse-leg congruence.
6. Therefore FB = FE because they are corresponding parts of congruent triangles.
You can use the same proof for EG and GC.
Now, what if the figure looks like these?
Want more geometry problems? Click here. For geometry theorems with proofs, just click the link.
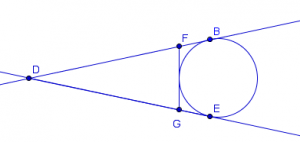
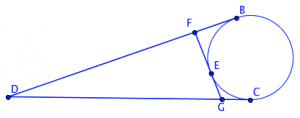
Here is another tangent-to-a-circle problem:
https://docs.google.com/file/d/0B6lw97EHbvfHMTF2LXVycW51b3M/edit
Where to find the solution to the above problem???