Theorems and Problems on Angles of Triangles
Here are three important theorems about triangles: sum of angles of a triangle, the measure of the exterior angle, and the base angles of an isosceles triangle. Sample problems where these are applied are also provided. The problems involved the concept of ratio.
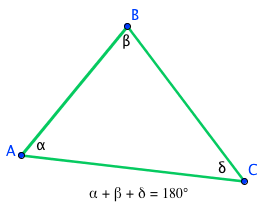
Theorem: The Sum of the Angles of a Triangle
The sum of the measures of the angles of a triangle is 180°.
In the figure, ?+?+? = 180°.
Problem 1: If the measure of the angles in a triangle is in the ratio 1:2:3, what is the measure of the biggest angle?
Solution: Let x be the smallest angle. It follows that the next bigger angle has measure 2x and the biggest angle has measure 3x. Their sum is x + 2x + 3x = 180°. This simplifies to 6x = 180° and x = 30°. The biggest angle, 3x, is 3 × 30° = 90°.
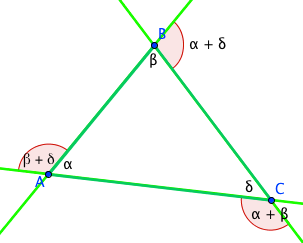
Theorem: The Exterior Angle of a Triangle
The exterior angle of a triangle is equal in size to the sum of the interior opposite angles.
Let ?, ?, and ? be the measures of the angles of a triangle. The exterior angle of the triangle at A is equal to ? + ?; at B is ? + ? ; and at C is ? + ?.
Problem 2: If the measure of the angles in a triangle is in the ratio 1:2:3, what is the measure of the exterior angle at the second to the biggest?
Solution: From the solution to problem 1, we know that the smallest angle is 30° and the biggest angle is 90°. Therefore the exterior angle at the second biggest angle is 30° + 90°.
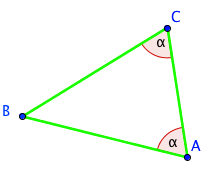
Theorem: The Base Angles of an Isosceles Triangle
The base angles of an isosceles triangle are equal.
In the figure, ?ABC is an isosceles triangle. The two equal sides are AB and BC. The base angles A and B have equal measure. That is , ? = ?. The third angle, angle B in the drawing below, is called the vertex angle.
Problem 3. If the ratio of the measure of the vertex angle to the base angle of an isosceles triangle is 2:1, what is the measure of the vertex angle?
Solution: Since base angles of an isosceles triangle are equal and it is given in the problem that the ratio of the vertex angle to one of the base angles is 2:1, the measure of the angles of the triangle is in the ratio 2:1:1. Let x be the measure of the base angles. This implies that x + x + 2x = 180°. This simplifies to 4x = 180° and x = 45°. Thus, the vertex angle is 2(45) = 90°.
Proofs of theorems will be in the next few posts.
[suffusion-widgets id=’1′]
???
Lenghts (1*a), (2*a), (3*a) of consecutive segments … makes a rectangle triangle, yes or no?
(3*a)^2 does or doen’t equal [ (1*a) + (2*a) ]^2 ?
Then… What’s the meaning of your phrase: ‘We certainly do not use the convention 1a, 2a, 3a for lenghS [of the sides] of [the] Rectangle Triangle’ ?
Thank you for your comments. In our country, we don’t have that convention of naming angles or vertices consecutively using letters of the alphabet be it English or Greek. Triangle bearing the initials of the teacher and quadrilateral LOVE (especially in February) are common labels we use. We can read them clockwise or counterclockwise depending on the agreed rules, if the teacher imposes one. We certainly do not use the convention 1a, 2a, 3a for length of Rectangle Triangle, if I understand what you mean. We don’t even call it that way. 🙂
121224: On triangles and ANGLES.
http://math-problems.math4teaching.com/theorems-and-problems-involving-triangles/
Congratulation for this beautiful display of basics of geometry! Words coming down bellow are no critics but a mere normal reader contribution, in the hope of improving your work.
On chapter 1 & 2, ‘Interior angles’ & ‘Exterior angles’, statement & figure: Greek caracters rank alpha, beta, GAMMA, delta, epsilon, … You have posited angles names ‘alpha’, ‘beta’, ‘delta’, in low case. (You have hushed ‘gamma’ up).
On chapter 1, ‘Interior angles”, exercise 1, paragraph 2: I’d rather turn it this way: (…) the next bigger angle MEASURES 2x, and the biggest angle MEASURES 3x. Where from: ANGLES MEASURES SUM UP TO x + 2x + 3x = 6x = 180°. Then x = 180° / 6 = 30°, and the biggest angle = 3x = 3 * 30° = 90°.
Input of this experiment: One of many other easy means of drawing a RECTANGLE TRIANGLE is to impose sides lenght 1a, 2a, 3a. (‘a’ being the lenght unit).
Search the other ‘easy means’!
Do you want me to continue this proofreading your work?