Trigonometric equations and their graphs

The general technique in matching trigonometric graphs and equations is to consider the intercepts, the minimum and maximum points, the shape of the prototype graph and the transformations done to the graph.

Problem

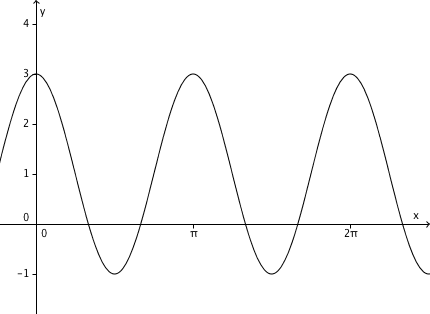
If 0?x?2? which one of the following trigonometric equations best describes this graph?

A. y = 3cos 2x

B. y = 2+cos 2x

C. y = 1+ 2cos 2x

D. y = 2+2 cos x/2

E. y = 1+2sin 2x

I’m sure you are not one of those who will choose E. The question is not “Which is different?” But many students have fallen to that.

Solution:

You can look at the y-intercept or you can start by the over all shape of the graph. If you look at the y intercept, it’s value is 3 (of course it’s at at x=0). Option A is possible since 3cos 0 = 3(1)=3. Option B is possible since 2+cos 2x = 2+1 = 3. Option C is possible since 1+2(1)= 3. Option D is NOT possible since 2+2(1)= 4. Option E is NOT possible since sin 0 = 0 so 1+2sin2x = 1+2(0)=1. These leaves you options A, B, and C which are all cos 2x. All you need to do now is to interpret the transformation of the graph of cos 2x.

The period of the cosine graph is 2 and its amplitude is also 2.  The graph must have an equation of the form y = a 2cos 2x. Now, 2cos 2x if x = 0 is 2. Thus, to have y = 3 you must add 1 to the equation. The correct answer is y = 1 + 2cos 2x.

Definitions:

The amplitude of a periodic function is the maximum displacement of the graph from the x-axis in either the positive or negative direction.

The period of a periodic function is the horizontal distance necessary to make one complete cycle of the graph.