What is Conditional Probability?
 The conditional probability of an event B is the probability that the event will happen given the knowledge that an event A has already happened. This probability is written P(B|A), notation for the probability of B given A. In the case where events A and B are independent, the conditional probability of event B given event A is simply the probability of event B, that is P(B).
The conditional probability of an event B is the probability that the event will happen given the knowledge that an event A has already happened. This probability is written P(B|A), notation for the probability of B given A. In the case where events A and B are independent, the conditional probability of event B given event A is simply the probability of event B, that is P(B).
If events A and B are not independent, then the probability of the intersection of A and B (the probability that both events occur) is defined by
P(A and B) = P(A)P(B|A).
From this definition, the conditional probability P(B|A) is easily obtained by dividing by P(A):
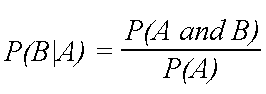
The equation above is of course only valid if P(A) is not equal to 0. If the formula looks daunting, the following video will help you understand it. Thanks to Khan Academy. This one is great.
The Bayes’ Theorem gives a way of calculating P(A|B) given the knowledge that P(B|A) has already happened. Bayes’s formula is defined as follows:
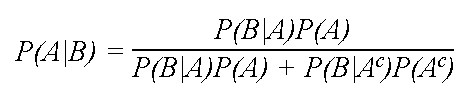
Sample problem in my next post.
Good and interesting, except… You break the rule we pain so much to try to inculcate our pupils: You have popped an element in – the letter C, in the terminal formula by Bayes – which you have omited to introduce! Grr! 😉