Application of Distributive Property
What is the Distributive Property?
The distributive property (aka distributive law) is a property of real numbers which says that the product of a number say a and the sum (or difference) of two numbers say b and c, is equal to the sum (or difference) of the product of a and b and a and c. In symbol, we have:
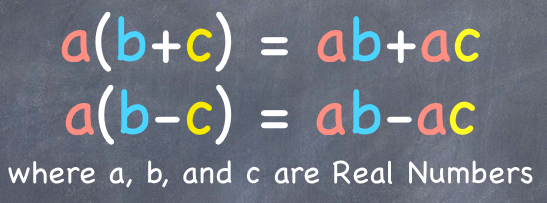
I’m sure you have used this property to work with numbers. A typical question that involves the distributive property would be: Find the product of x and (x-7). Using the distributive property, you will get . This means that if x = 10, one way to calculate the product of 10 and (10-7) is 10×3 or 10×10-70. Both of these will give you 30. This property is true for all real numbers.
Here’s a more interesting problem where you can apply the distributive property of real numbers.
Problem
Warning: You do not need your calculator for this.
Solution
I’m not going to give the solution for each. Instead I’ll use a general form. I say general because it has the same structure as the three problems. The x represents any real numbers.
=
=
=
This in fact works for n number of terms. You can try proving the statement below to show that it is true for n terms in any x.
Prove
or
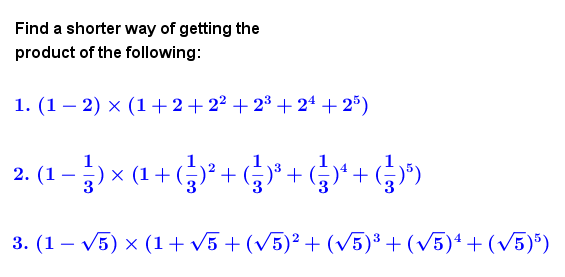
This can also be used to create a fake-proof that 1+1+1…+1 = 1.As a exercice you could ask your students to show what’s wrong with the of the following argument:
Consider the sum:
1+x+x²+x³+…+x^n = 1
We want to find a number x such that the above equation is solved. Then, f we multiply both sides by 1-x we have:
(x-1)(1+x+x²+x³+…+x^n) = x-1
Then, by the above formula:
x*x^n – 1 = x – 1
Cutting out the -1:
x*x^n = x
So we cut out a x in both sides:
x^n=1
Therefore, x = 1. But if we put this value in the original sum:
1+1+1²+1³+…+1^n = 1
By the way, that’s a cool way of looking into the geometric progression sum formula!
Bravo Erlina! Encouragements to pursuit!
Jean-Yves Rollin, Skype scolaire75