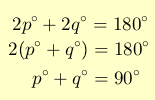Proofs of angle in a semicircle theorem

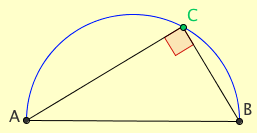The Angle in a Semicircle Theorem states that the angle subtended by a diameter of a circle at the circumference is a right angle. An alternative statement of the theorem is the angle inscribed in a semicircle is a right angle.

Proof

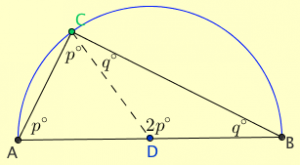
Draw a radius of the circle from C. This makes two isosceles triangles. Because they are isosceles, the measure of the base angles are equal. Let the measure of these angles be as shown. /CDB is an exterior angle of ?ACB. By exterior angle theorem, its measure must be the sum of the other two interior angles.

Now all you need is a little bit of algebra to prove that /ACB, which is the inscribed angle or the angle subtended by diameter AB is equal to 90 degrees.

Of course there are other ways of proving this theorem. You can for example use the sum of angle of a triangle is 180. Angle CDA = 180 – 2p and angle CDB is 180-2q. These two angles form a straight line so the sum of their measure is 180 degrees. That is (180-2p)+(180-2q)= 180. This simplifies to 360-2(p+q)=180 which yields 180 = 2(p+q) and hence 90 = p+q.

Click angle inscribed in a semicircle to see an application of this theorem. Click semicircles for all other problems on this topic.