Proof of Triangle Exterior Angle Theorem
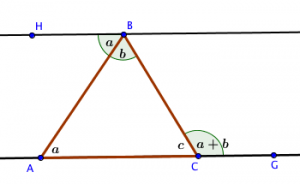
The exterior angle of a triangle is the angle that forms a linear pair with an interior angle of the the triangle. To draw the exterior angle all you need to do is to extend the side of the triangle. A linear pair is a pair of angle that forms a straight line. In the figure below angle BCG is the exterior angle. It forms a linear pair with angle ACB.
Problem: If the interior angles of ?ABC has measure a, b, and c, what is the measure of exterior angle BCG?
Solution 1: (1/5 mark)
Get a protractor and measure it.
Of course I’ll give you a 5 out of 5 mark for this solution if you are a 4th or 5th grader.
Solution 2: (5 out 5 marks)
Construct a line parallel to AC. With AB as transversal, angle HBA = angle BAC because they are alternate interior angles. The same reasoning goes with angle HBC and BCG which are also alternate interior angles hence will have the same measure, a+b.
We just proved in solution 2 an important theorem in Geometry called The Exterior Angle Theorem. You can use this theorem in solving many geometry problems involving triangles and other polygons.
Exterior Angle Theorem states that in a triangle, the measure of an exterior angle is equal to the sum of the two remote interior angles.
You can use the exterior angle theorem to prove that the sum of the measures of the three angles of a triangle is 180 degrees. Can you set up the proof based on the figure above? If you want to know other proofs for sum of angles in a triangle, click the link.