Three proofs that the sum of angles of a triangle is 180
Theorem. The sum of the interior angles of any triangle is 180°.
Here are three proofs for the sum of angles of triangles. Proof 1 uses the fact that the alternate interior angles formed by a transversal with two parallel lines are congruent. Proof 2 uses the exterior angle theorem. Proof 3 uses the idea of transformation specifically rotation.
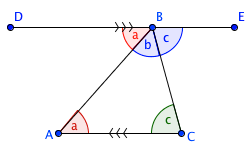
Proof 1
Construct a line through B parallel to AC. Angle DBA is equal to CAB because they are a pair of alternate interior angle. The same reasoning goes with the alternate interior angles EBC and ACB.
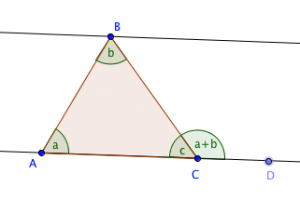
Proof 2
This is similar to Proof 1 but the justification used is the exterior angle theorem which states that the measure of the exterior angle of a triangle is the sum of the measures of the two remote interior angles. In the diagram, angle A and angle B are the remote interior angles and angle BCD is the exterior angle. Click this link for the proof of the exterior angle theorem.
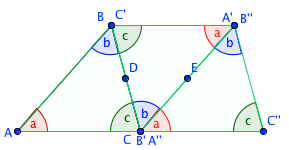
Proof 3
Rotate ?ABC 180° clockwise about D the midpoint of BC. This rotation produces the image ?A’B’C’. Rotate the image again by 180° clockwise but this time about E, the midpoint of A’B’. In the figure you can see that a+b+c forms a straight line and hence measures 180°.
@Denise and Jeff. Here’s a link to the applet I created for Proof 3. http://curriculum.nismed.upd.edu.ph/2013/03/dynamic-worksheet-for-teaching-geometric-relations/. You are right Jeff, it creates parallelogram and can be used as materials for teaching other geometric relations.
Proof 3 relates to what we do in grades 4-6: Create triangles on paper, tear off the corners (angles), and align them to create a baseline, hence sum =180º.
I do like that, in proof 3, one creates parallelograms, and can see that alternate interior angles are congruent.
A couple of questions:
Proof 2: Isn’t the fact that the angles add up to 180 degrees used in proving the exterior angle theorem? Well, that’s the way we did it in my geometry class (uber-many years ago), but there’s always more than one way to prove a theorem — so how *would* you prove the exterior angle theorem without using this sum?
Proof 3: I don’t remember much about rotations, since my geometry class just skimmed over that chapter. How do you know for sure that this technique forms a straight line?
Hi Denise,
Yes some of our books also do that. They use the idea of sum of angles of triangles to prove the exterior angle theorem. But in cases where the former has not been proven, we use the idea of alternate interior angles and linear pair to prove the exterior angle theorem. Pedagogically, the latter should be the case. The proof of the exterior angle simply becomes one of the application of alternate interior angles. Thanks for your comment. I was inspired to make a post about the proof of exterior angle theorem.
I will write another post for your query re Proof 3. Thank you.
Just a minor edit:The same resigning goes the
resigning should be reasoning
Thank you. I will correct it.