Theorems on Centroid, Orthocenter, and Circumcenter

Here are three important theorems involving centroid, orthocenter, and circumcenter of a triangle. This is part of the series of posts on theorems in secondary school geometry. Proofs of the theorems and application problems will be provided in the next few posts.

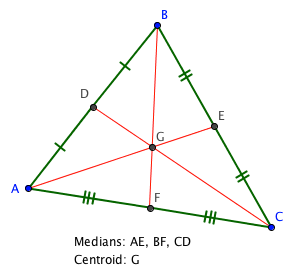
Theorem: Centroid Theorem

The lines joining the vertices of a triangle to the midpoints of opposite sides (medians) are concurrent and trisect each other.

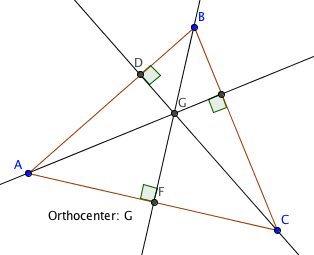
Theorem: Orthocenter Theorem

The three altitudes from the vertices to the opposite sides of a triangle are concurrent.

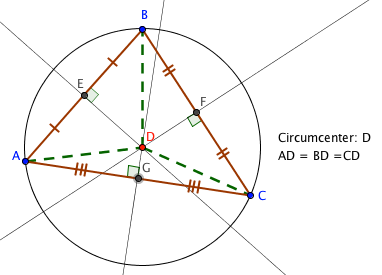
Definition: Circumcenter

The three perpendicular bisectors of the sides of a triangle meet in a single point, called the circumcenter.

Theorem: Circumcenter Theorem

The vertices of a triangle are equidistant from the circumcenter.

Note: In the figure, D is the circumcenter of the triangle as well as the center of the circle. Can you see that AD, BD, and CD are radii of circle D. How’s that for hint for the proof of the theorem?

Click Perpendicular Bisectors for application of this theorem in a problem.

The Euler Line

In the 18th century, the Swiss mathematician Leonhard Euler noticed that three of the many centers of a triangle are always collinear, that is, they always lie on a straight line. This line has come to be named after him – the Euler line.

Check out the other theorems:

[suffusion-widgets id=’1′]