Theorems on Triangles with Proportional Sides

This is the second in the series of posts about important and useful theorems in secondary school geometry. The first set of theorems is about angles of triangles. This second set involves the proportional sides of similar triangles. Proofs and sample problems will be provided in the next few posts.

Definition: Similar Triangles

Two triangles are similar if the corresponding angles are equal.

Definition: Converse

The converse is a statement where the two main ideas of a given statement is interchange.

Note: Sometimes the converse of a statement is true and sometimes it is false. The contrapositive is always true.

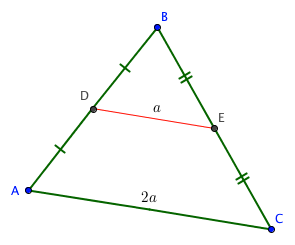
Theorem: The Midpoint Theorem and its Converse

The line joining the midpoints of two sides of a triangle is parallel to the third side and half its length.

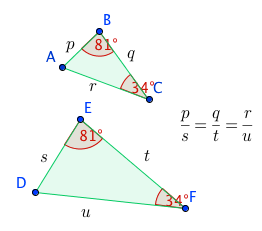
Theorem: Similar Triangles Theorem and Its Converse

If two triangles are equiangular, their corresponding sides are proportional.

Converse: If the corresponding sides of two triangles are proportional, then the two triangles are similar.

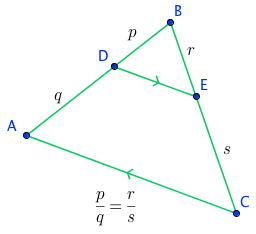
Theorem: Parallel Within Triangle Theorem and its Converse

If two sides of a triangle are cut proportionally by a straight line, then this line is parallel to the third side.

Converse: If a straight line cutting the two sides of a triangle is parallel to the third side, then the two sides are cut proportionally.

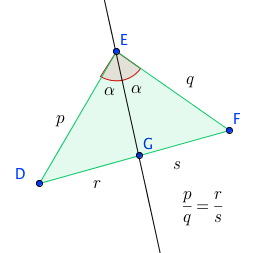
Theorem: The Bisectors of an Angle of a Triangle

The bisectors of the angle of a triangle divide the opposite sides in the ratio of the sides containing them.

Proofs and sample problems will be provided in the next few posts. Meanwhile you may want to know about other geometry theorems.

[suffusion-widgets id=’1′]