Squares, Triangles, and Van-Aubel’s Theorem

Problem

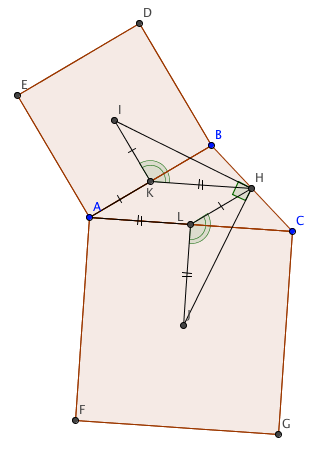
In the figure, H is the midpoint of side BC of ?ABC. The points I and J are the intersection of the diagonals of square ABDE and square ACGF respectively, that is they are the centers of the square. Prove that IH and HJ are congruent and that angle IHJ is a right angle.

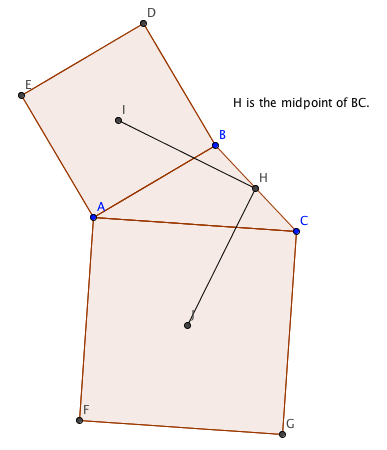Proof

You supply the text :-). You will need the mid-segment theorem.

Challenge Problem:

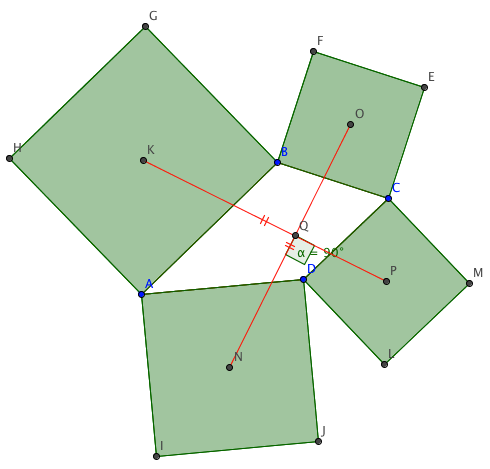
Squares are drawn on the the side of the quadrilateral. K, O, P, and N are the intersections of the diagonals of the square. Prove that KP = ON and that they are perpendicular to each other.

This challenge problem is actually called the Van-Aubel Theorem which states that that the two line segments between the centers of opposite squares constructed at the side of a quadrilateral are of equal lengths and that the lines through the centers are at right angles to one another. I created the first problem as hint towards one of its geometric proof. This theorem can also be proved using vectors and complex numbers.