How to Prove the Central Angle – Inscribed Angle Theorem

When two secants intersect on the circle, it forms an inscribed angle. There are three cases in which the secants may be positioned as shown in the figure below. These positions form different cases for the central angle-inscribed angle relationship. So when you prove the theorem that the measure of the inscribed angle is half the measure of the central angle intercepting the same arc as the inscribed angle, you need to show that this is indeed true for each case since it is not very obvious that indeed it is true to all these cases.

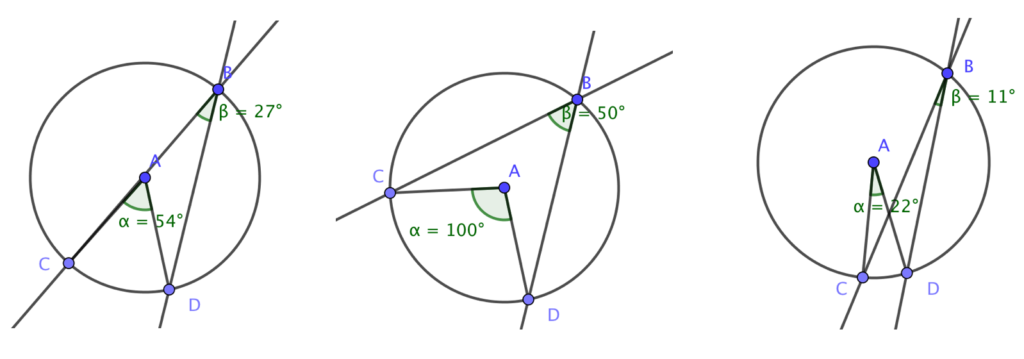
I constructed the circle diagrams using GeoGebra and so I did not make up the actual measure. They are the actual measures of the angles. Observe that the measure of the inscribed angle is half the measure of the central angle intercepting the same arc. But these are specific measure and so you should wonder whether this relationship holds for any inscribed-central angle and for all of the three cases shown in the figure above. You need a proof to establish the generality of the conjecture. In fact, this conjecture is one of the most important theorem in secondary school geometry.

Theorem: The measure of the inscribed angle is one-half that of the central angle intercepting the same arc.

Proof of Case 1 (in Figure 1)

We need to prove that ?CBD = ½?CAD. This means that we need

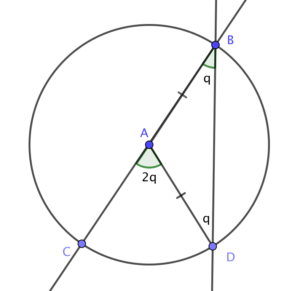
to express the measure of?CBD in terms of?CAD.

We can claim that ?CAD is isosceles because it’s two sides have the same length being radii of the circle.

Let q be the measure of ?CBD.

If this is the case then ?ADB = q also since the base angles of any isosceles triangle have equal measures.

We can also claim that ?CAD = 2q since it is the exterior angle ?CAD and its measure is the sum of the two remote interior angles. [This is the exterior angle theorem.]

Because ?CBD = q and ?CAD = 2q, and q is one-half of 2q we can say that ?CBD = ½?CAD which is what we want to prove.

Note that in some books and in some curriculum like in the United States and the Philippines, the measure of the intercepted arc is defined in terms of the measure of the central angle. 

Postulate: The measure of the central angle is equal to the degree measure of the intercepted arc.

Thus, the central-inscribed angle theorem is also stated as:

Theorem: The measure of the inscribed angle is half the degree measure of the intercepted arc.

Try proving the other two cases above to practice your skill in proving. Pay attention to the structure of the proof. You first state what you want to prove. Make the corresponding drawing or representation to show what you are doing. And lastly, be conscious of what you claim. They should always have a corresponding substantiation that would make your claim legitimate.

You may also want to see the an extension of this theorem on angles on semicircle. If you are a teacher you may also want to know more about teaching proofs and proving.